1. Compressive Video Sensing & Classification
2. GPU accelerated CVS
3. Compressed Gated Range Sensing (CGRS)
4. Compressed Sensing & Sparsity in Imaging
5. Compressed Sensing in Localization
6. Fundamentals of CS Acquisition and Reconstruction

Recovery of Quantized Compressed Sensing Measurements

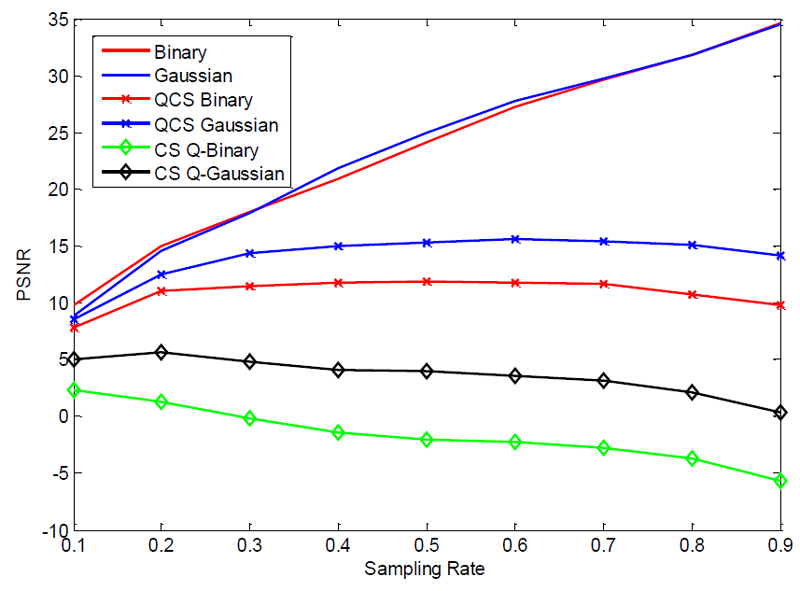
Compressed Sensing (CS) has revolutionized modern signal and image acquisition architectures ranging from one-pixel cameras, to range imaging and medical ultrasound. Although signal sampling and reconstruction are crucial, systems that implement CS must use a finite number of distinct symbols, via a quantization process, in order to efficiently store and transmit the measurements. We considered a novel formulation of CS recovery where the effects of quantization are taken into account during reconstruction. Formally, we consider a non-linear mapping function of the sparse signal given where recovery is achieved by solving a modified greedy minimization problem with additional constraints on the consistency of the recovered signal with respect to its quantized counterpart.

Compressed Sensing Reconstruction of Convolved Sparse Signals

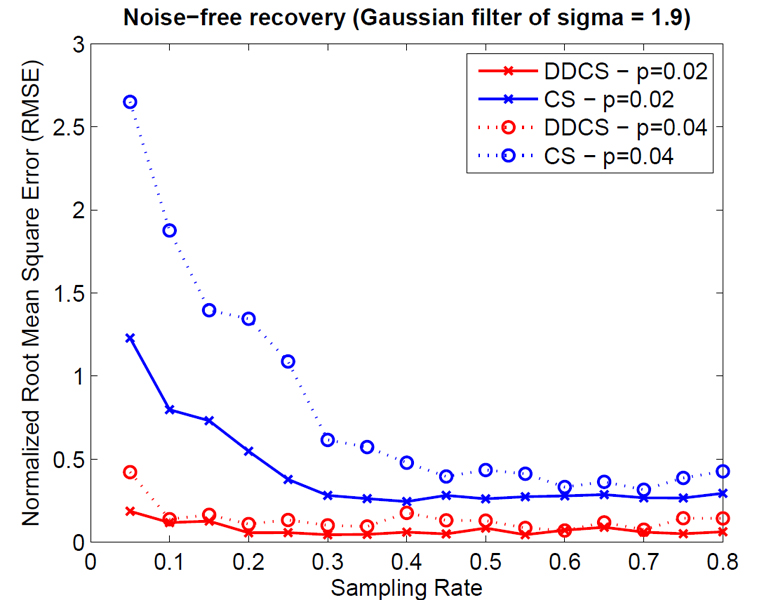
A large number of signals, ranging for neuronal activity to range imaging and radar, can be modeled as time series of shifted and scaled pulses. By modeling the pulses as series of spike (delta) functions, the CS theory suggests that recovery is possible provided enough random measurements are taken and the sampling matrix adheres to the RIP property.  However, blurring caused by signal propagation and the sampling process will distribute the signal's energy to a larger support, resulting in significantly less sparse signals, necessitating higher CS sampling rates. We investigated an extension of CS theory that in addition to the temporal sparsity of the signal, also assumes the existence of a dictionary that is able to sparsely represent the low pass filtering signal. Our method differs from previous approaches in that we assume that a parametric model of the convolution function is known and the specific realization is of interest. This model encodes a more general class of problems such as blurring caused by the lens of an imaging system.